

In this example, we have found out the area of cutting and filling for all the 6 Sections using the Trapezoidal Method at formation level 20. The volume of a prism can be obtained by multiplying its base area by total height of the prism. Solution: Volume Ah 25 cm 2 × 9 cm 225 cm 3. Example: Find the volume of the following right prism. Worksheet to calculate volume of prisms and pyramids.
where A is the area of the base and h is the height or length of the prism. However, lets say that we cut a slice from the rectangular prism. The volume of a right prism is given by the formula: Volume Area of base × height Ah. The estimation of earthwork gives nearly an accurate volume. We know that the volume of a rectangular cylinder is V l w h. Prismoidal formula is accurate in finding the volume of prisms, pyramids, wedges, and prismoids having irregular end sections.
#Volume of trapezoidal prism series
If there are a series of areas A1, A2, A3,….An at regular interval L, The average end area calculation is used to calculate the volume between two cross-sections i.e., Two cross-sectional areas are averaged and multiplied by the length (distance) between two cross-sections to get the volume. L – Distance in meters A1 and A2 – area in Square meters The formula for calculation of volume by average end area: Once the section-wise area calculation is done using section method, any of the 3 Volume calculation methods can be used for Volume CalculationĪverage End Area Volume Calculation (Trapezoidal Method) I'm not sure whether you are expected to know this though.Volume Calculation for Areas found using Section Method

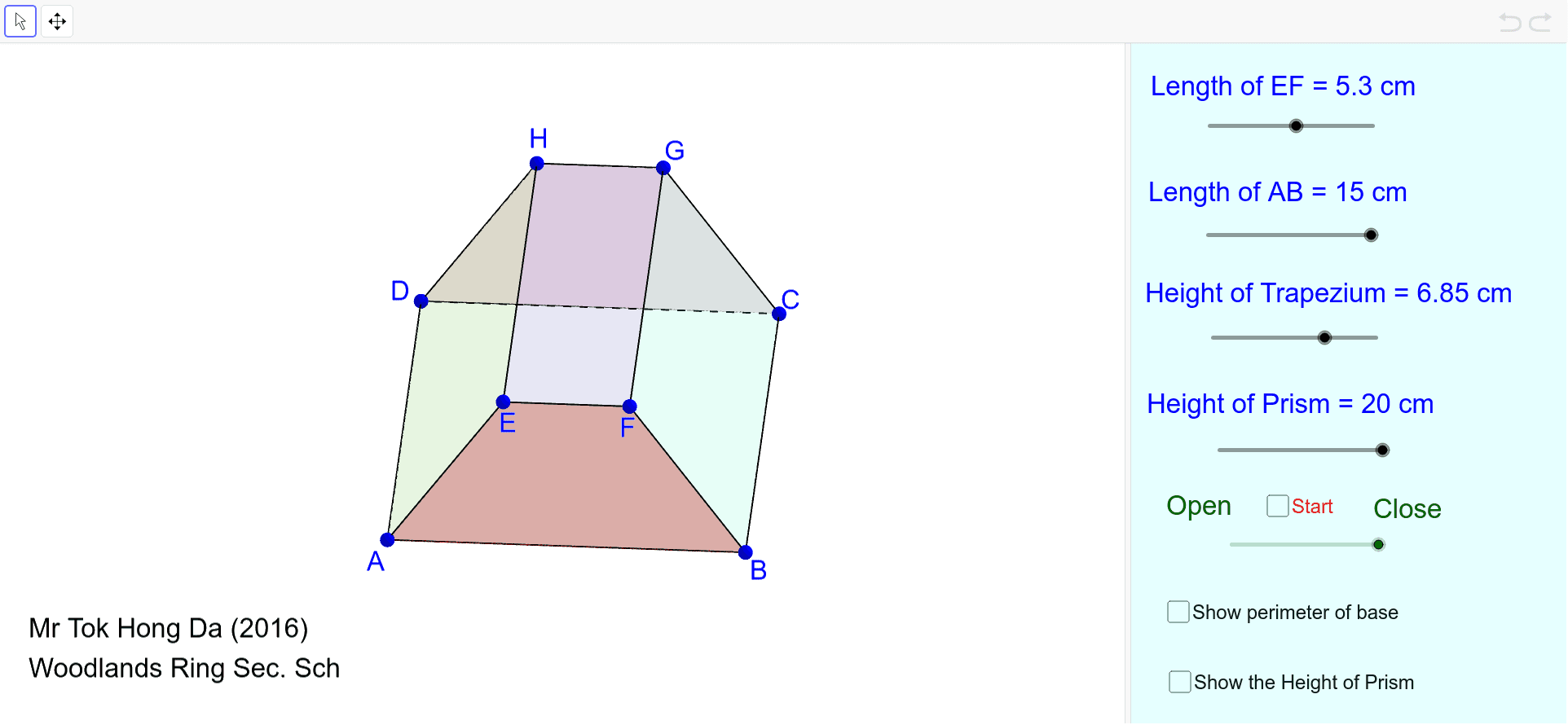
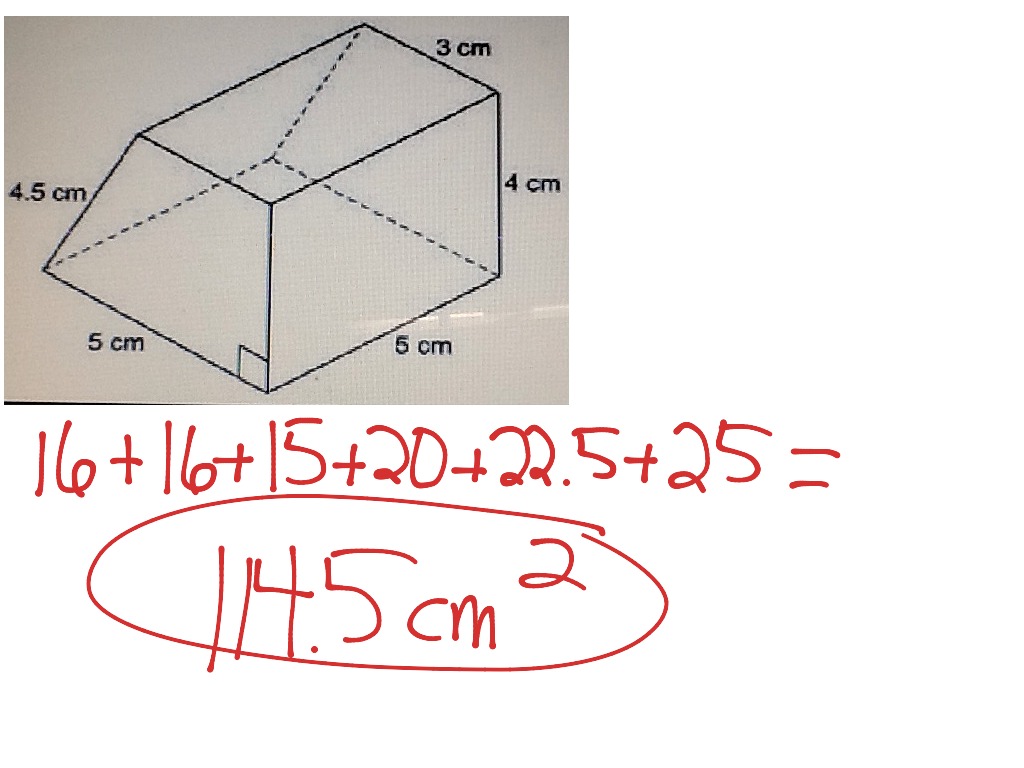
In general the formula to compute such a shape with height $h$, top rectangle $a\times b$ and bottom rectangle $c \times d$, with the $a$ side parallel to the $c$ side, is $\frac16 h(2ab+2cd+ad+bc)$. what is the formula for the surface area of a trapezoidal prism SA2(base area)+area of lateral sides. Assuming the faces are still plane, the cross-section at height $x$ (measured in $m$) is given by $(10-x)\times(8-\frac 32 x)$, and the volume can be determined by integration to yield $V = \int_0^2(10-x)(8-\frac 32 x)dx = 118 m^3$. If the top and bottom faces of the stack are laid out as hinted in the question, with the bottom $10m$ parallel to the top $8m$ and the bottom $8m$ parallel to the top $5m$, it is neither a trapezium prism nor a truncated pyramid, because the non-horizontal edges do not intersect in a single point. In case the $8m$ on top and bottom are parallel, you have a trapezium prism, with trapezium area $(10m+5m)/2 \times 2m$ and "height" $8m$ (perpendicular to the trapezium), resulting in a volume of $120 m^3$. You can calculate it by using this formula: volume ((short base length + long base length) / 2) × height ×. Furthermore the question might be ambiguous whether the $8m$ edge of the top face is parallel or perpendicular to the $8m$ edge of the bottom face, and this affects the final result. The volume of that trapezoidal prism will be 1 m. The pyramid-based answers do not work because the trapezoidal prism is not actually part of a pyramid: the non-horizontal edges do not meet in a single point. Identify the parallel sides of the base (trapezoid) to be $b_ Step 2 : Volume of the given prism is base area x height or V B x h Step 3 : Find base area. So, the given prism is a trapezoidal prism. If we consider one of the trapezoid side walls as base, the height of the prism would be 22 cm. I am confused what is the correct approach. Solution : Step 1 : In the given prism, the two side walls are trapezoids. I saw online different methods giving different answers to this question. I also assume a prism is the same thing as a pyramid for geometrical purposes.Ī trapezoidal prism is a 3D figure made up of two trapezoids that is joined by four rectangles. Let’s say that one knows the top and bottom width values, length, and height of the figure. I only confusion I have about this problem is the calculation of the volume of the stack which I believe is the trapezoidal prism (or truncated (right) rectangular prism or frustum of (right) rectangular prism). Volume of a Trapezoidal Prism By referring to the above diagram, all the components of a trapezoidal prism are understood. I know the approach needed to solve this problem. A water trough is 6 m long and its cross-section is an isosceles trapezoid which is 100 cm wide at the bottom and 200 cm wide at the top, and the height is 50 cm. By how many centimetres can the level be raised? For a plot of land of 100 m × 80 m, the level is to be raised by spreading the earth from a stack of a rectangular base 10 m × 8 m with vertical section being a trapezium of height 2 m.


 0 kommentar(er)
0 kommentar(er)
